Keywords: graphite; thin film; thermal diffusivity; flash method
TPP035
Abstract
This paper describes in detail the relevant theory and experimental design of measuring the in-plane thermal diffusivity of high thermal conductivity graphite thin film samples with TA Instruments’ flash diffusivity analyzer DXF 200. Thin film graphite is commonly used as part of a battery’s heat management system because graphite can serve as an efficient heat transport material. The experiment was repeated several times on a graphite thin film with a thickness of 25 μm. The reliability of the system was proved by verifying the thermal diffusivity of the standard graphite sample. Eight pulse tests on the graphite thin film showed a close fit between the experimental data and the theoretical model as well as excellent repeatability. Graphite is used as part of a heat management system because it can efficiently transport heat away from the center of a battery pack and towards an external heat sink.
Introduction
Lithium-ion batteries are the dominant rechargeable battery technology on the market today for many applications including consumer electronics, electric vehicles, and industrial equipment. The dominance of lithium-ion batteries over other rechargeable battery technologies such as nickel metal hydride (NiMH) and lead acid include a higher energy density, lower self-discharge rate, low maintenance requirements, and higher voltage per cell (around 3.6 V compared with 2 V per cell for lead acid).
Although lithium-ion batteries offer many advantages over competing rechargeable battery technologies, their main disadvantage is that they require active thermal and circuitry management (i.e. protection from under- and overcharging).
The typical operating temperature of a lithium-ion battery is between -20 to 60 °C with 20 to 40 °C considered as optimum. To stay within this optimal range, active temperature management systems are often employed. In addition to active thermal management, appropriate battery material selection can aid heat transport which can improve battery lifetime, performance, and safety.
Hence, material science, and in particular, thermal analysis during material design and selection, plays a crucial role in battery thermal management. Researchers employ thermal diffusivity measurements because thermal diffusivity describes the rate of temperature spread through a material. Understanding the thermal diffusivity of a battery material can help with material selection and the development of thermal interface materials, thereby leading to more efficient heat removal in working batteries. This paper will illustrate how thermal diffusivity of a graphite thin film can be determined using flash diffusivity.
Application Benefits
- The flash method is the most effective method for measuring the thermal diffusivity of heat management materials typically used in lithium-ion batteries.
- Features short measurement time, excellent accuracy and high repeatability, and is completely non-destructive to materials.
- The flash method applies pulses of energy from a laser or xenon lamp uniformly to the front surface of a small-sized sheet sample.
- High-speed data collection is performed with a sensor to record temperature changes over time on the back surface of the sample.
Experimental Principle and Design
A flash diffusivity analyzer, specifically a DXF 200+ (TA Instruments, USA), was used for related experimental design and data analysis.
The standard thermal diffusivity of a sample is obtained with a thermal loss correction model, in which a uniform pulse across a sample face with known thickness results in a time-dependent temperature rise curve of the back surface of that sample. This is known as a through-plane method, as the pulse is measured through the vertical axis of the sample.
However, in recent years, the use of the flash method to measure the in-plane thermal diffusivity of micron-sized thin films (in which the same pulse is measured across the sample rather than through it) has become a challenging aspect in the characterization of thermal properties of materials. Due to the particularity of the sample size, compared with traditional materials, there is heat loss on both the upper and lower surfaces of the thin film. Therefore, commonly used correction models such as Parker, Clark & Taylor, Cape-Lehman, and Cowan are no longer applicable. It is necessary to find a new model to correct and fit the temperature rise signal. Additionally, the particularity of boundary conditions also leads to the complexity of thin film testing.
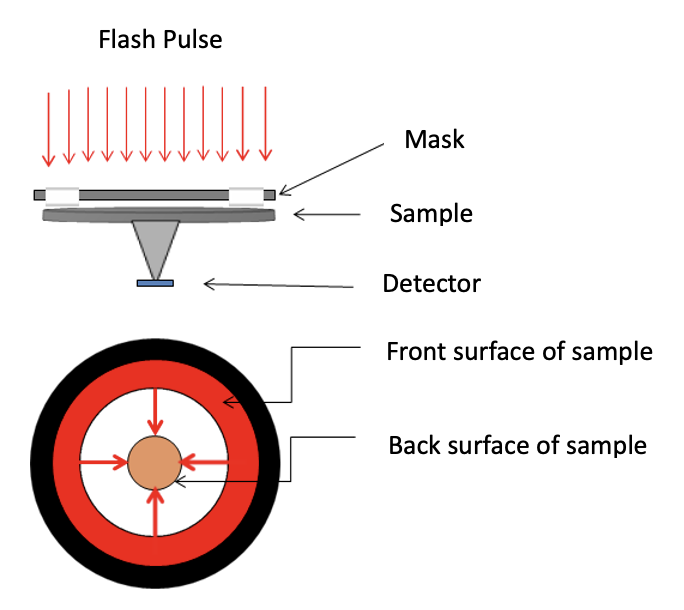
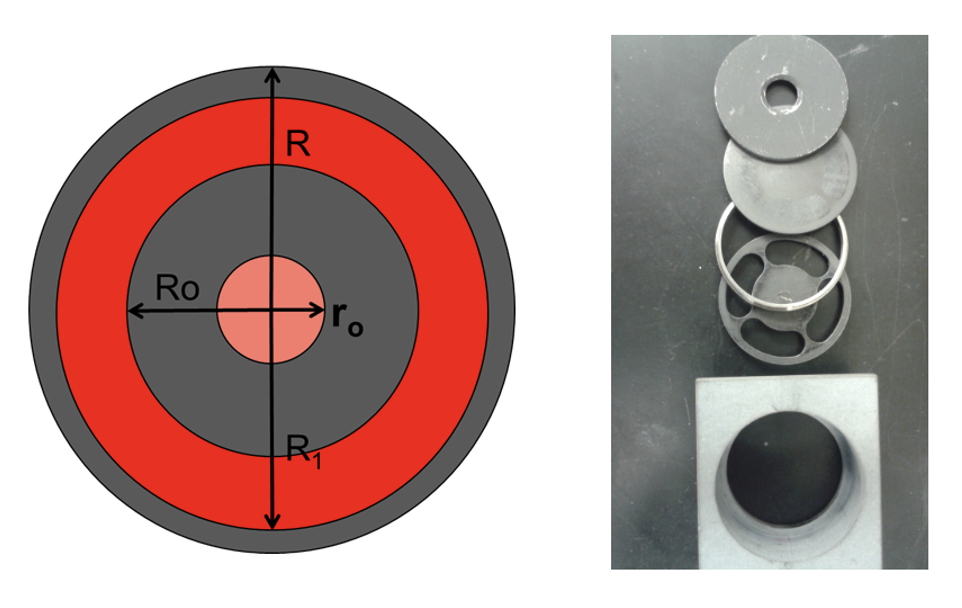
The test fixture for thin films and the corresponding correction model have been adopted to determine the measurement of in-plane thermal diffusivity of various film materials. The test principle and structure of the thin film fixture are shown in Figure 1. The xenon light applies uniform short pulses to the front surface of the fixture, which houses the sample. After the outer edge of the sample is heated, the heat transfers from the outer edge to the center of the circle along the thin film. At the center of the back of the fixture, a solid probe detector records the temperature rise signal at the center of the thin film sample. This assists in producing the thermogram graph that will determine the thermal diffusivity of the thin film material.
The Fin model is employed to correct the in-plane heat loss of the thin film. The relationship between the temperature rise signal T(t) and the transverse thermal diffusivity α (thermal diffusivity across the sample’s surface) is as follows (Equation 1):
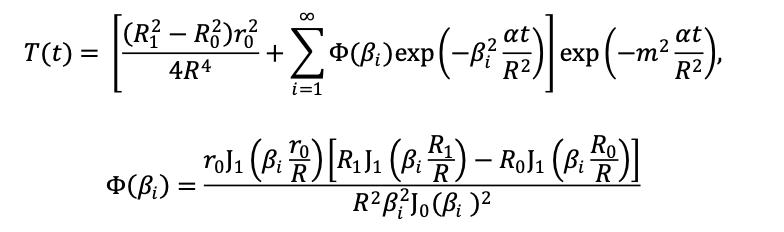
where α is the transverse thermal diffusivity, J0 and J1 are the Bessel functions of the first kind, β is the positive solution of the equation J1 (β)=0, and m is proportional to the ratio of the heat transfer coefficient to the thermal conductivity. In the Fin model, the temperature gradient along the thickness direction of the thin film sample is much smaller than the temperature gradient along the transverse direction of the sample. Therefore, it is not considered in the calculation of the temperature distribution. By introducing a parameter m proportional to the ratio of the heat transfer coefficient and the thermal conductivity, the heat loss on the surface of the thin film sample is calculated.
Repeated experiments have proved that the experimental data can be well corrected by using the Fin model. Thus, fitting that data obtained from the DXF 200+ flash diffusivity analyzer to the Fin model allows researchers to obtain accurate thermal diffusivity values.
Finally, before describing the experimental results, it should be noted that some applications may call for calculating the value of thermal conductivity in addition to thermal diffusivity. The relationship between thermal diffusivity (α), density (ρ), specific heat (Cp) and thermal conductivity (λ) is shown in Equation (2). Hence based on the relationship in equation 2, if the sample density is already known, the specific heat (Cp) of the sample can be measured by comparing it with a standard sample with known thermal property values to obtain the thermal conductivity of the sample. A differential scanning calorimeter (DSC) can be used to measure the specific heat (Cp) of the sample with a three-step method. Alternatively, a modulated DSC (MSDC) technology can also be used to achieve direct measurement of specific heat. Thus, a battery researcher can convert between thermal diffusivity and thermal conductivity as required.
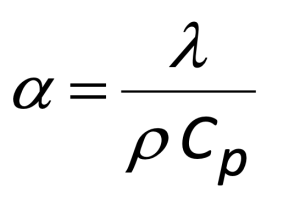
Measurement of In-Plane Thermal Diffusivity of a Graphite Film
Eight pulse experiments were carried out on a graphite thin film sample with a thickness of 0.0025 cm. The thermal diffusivity data obtained are as follows:
| Sample and Experimental Condition | Experimental Data of Thermal Diffusivity (cm2s-1) |
| Temperature: 25°C Thickness: 0.0025 cm |
8.934905 |
| 8.989135 | |
| 8.962159 | |
| 8.910634 | |
| 8.897129 | |
| 8.853366 | |
| 8.881133 | |
| 8.924013 |
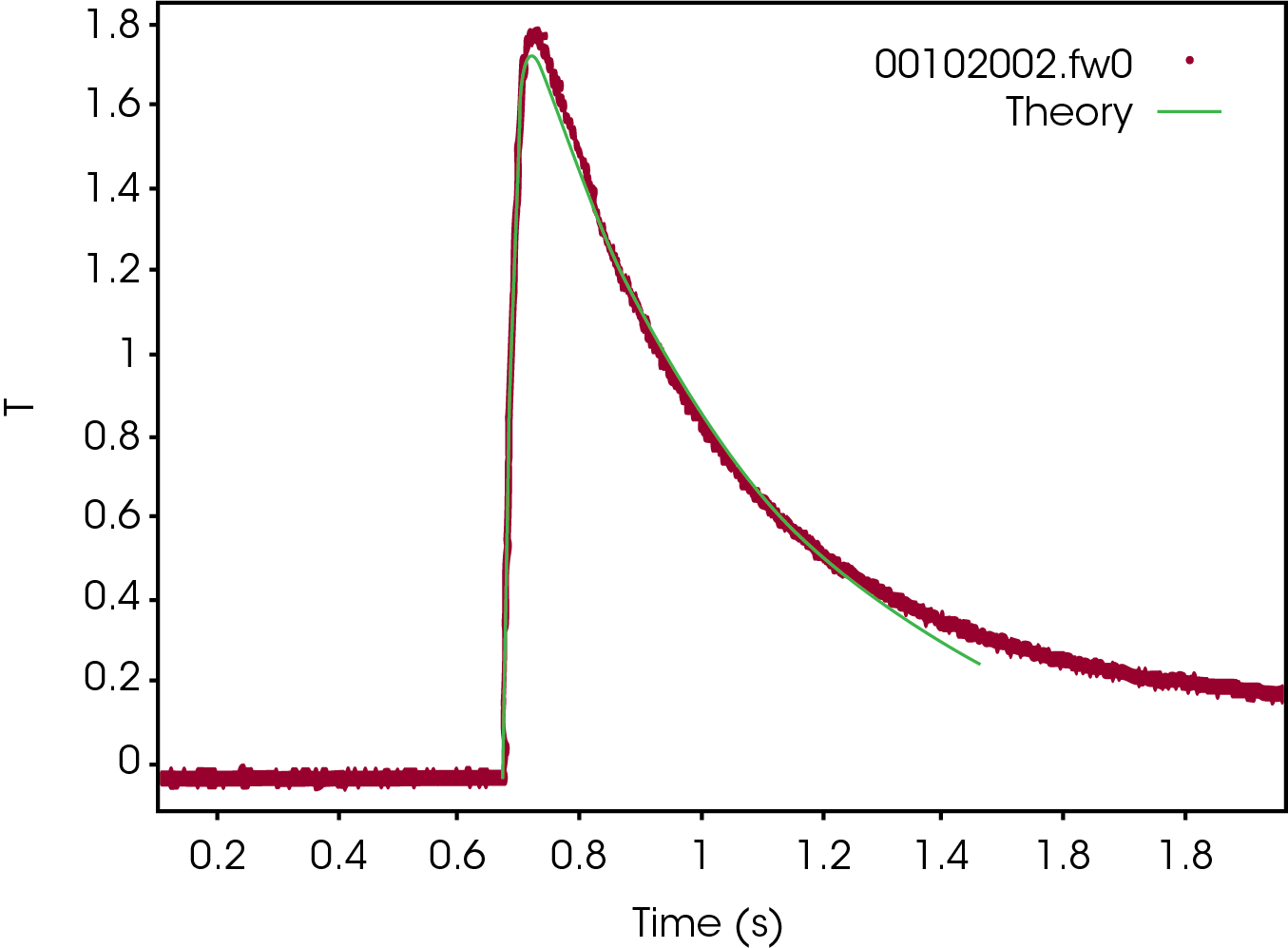
The original temperature rise curve of the graphite thin film sample is shown in Figure 3. The experimental data (red) fit very well with the Fin theoretical model (green), which proves the authenticity and validity of the thermal diffusivity data.
From the above, with a special sample fixture and model, the flash diffusivity analyzer is able to achieve accurate measurement of the in-plane (traverse) thermal diffusivity of micron-sized thin film samples. The measurement and analysis methods are simple and straightforward with high data reliability.
Conclusion
- Efficient heat removal represents a significant challenge in lithium-ion battery development.
- Thermal diffusivity is a very important parameter needed for designing a reliable thermal management system.
- Graphite is approximately 30% lighter than aluminum and has a higher thermal conductivity; hence, when graphite is used as part of a heat management system it can serve as an efficient means to transport heat away from the center of a battery pack and towards an external heat sink.
- Improving the thermal management capability of battery materials can ensure that battery components efficiently dissipate internally generated heat which can lead to an increase in battery lifetime, performance, and safety.
Acknowledgement
This paper was written by Qian Ma, Applications Manager, China at TA Instruments.
Click here to download the printable version of this application note.

