Characterizing Protein-Protein Interactions by ITC

Analyzing Protein-Protein Interactions

Crystal structures of protein complexes show that the interaction of two protein surfaces requires good hydrophobic, charge and shape complementarity, so that the resulting interface is as well packed as the interior of a protein. Given this requirement, coupled with prior knowledge of which proteins interact (for example, by using yeast twohybrid systems (Toby and Golemis, 2001), protein fragment complementation assays (Hu and Kerppola, 2003), or a combination of both techniques (Hazbun et al., 2003)), it should in theory be possible to predict the interfaces through which two proteins will interact, and the mechanism of binding. In practice, however, prediction is complicated by dynamic events occurring in both the protein and in the solvent.

The inter- or intramolecular interaction of two protein moieties often results in substantial structural changes not only in the vicinity of the interacting interfaces, but also distant from the site of contact (Ladbury and Williams, 2004). This results in altered hydrogen bonds, electrostatic and hydrophobic interactions, and in a significant rearrangement of bound water molecules. Prior to two protein surfaces interacting, water molecules associated with each protein face form organized hydrogen bond networks to polar regions of a protein’s surface, and highly structured clathrate-like arrangements adjacent to hydrophobic surfaces. When these protein surfaces interact, many of the organized water molecules are released into the bulk solvent, but others remain highly localized and tightly bound to specific locations on the interacting surfaces. These immobilized water molecules satisfy otherwise unmet hydrogen bond requirements to the interface, fill cavities, and mediate interactions between the opposing interfaces. Because of their highly localized and organized structure, these waters are believed to be critical to interfacial stability and specificity (Raschke, 2006). Indeed, it appears that, at least in some systems, water-mediated interfacial interactions are more specific and stable than interactions where water molecules are excluded from the protein interface (Ladbury,1996).

The interaction of any two protein interfaces will result in unique protein structural changes and in a unique rearrangement of water molecules distributed between the free and bound state. These solvent rearrangements result in both entropic and enthalpic changes to the system: for example, removing water from a non-polar surface requires breaking hydrogen bonds between the solvent molecules (which is enthalpically unfavorable), but the released water molecules are motionally less restricted (which is entropically favorable). Since the thermodynamics of interactions between molecular interfaces are determined by the number and type of bonds associating the two surfaces, the balance of the enthalpic and entropic effects provides a thermodynamic fingerprint of the interaction (Ladbury and Chowdhry, 1996).

ITC is the most direct and quantitative approach for characterizing the thermodynamic properties of proteinprotein interactions (Doyle, 1997; Pierce et al., 1999; Jelesarov and Bosshard, 1999). Although other techniques allow the binding affinity and stoichiometry to be determined (Lakey and Raggett, 1998), none are as direct as ITC. For example, spectroscopic studies often require the use of labels, surface plasmon resonance requires immobilization (which can interfere with binding) and analytical ultracentrifugation is time consuming; additionally, the enthalpy of binding cannot be directly measured by any of these approaches, but must be calculated from the van’t Hoff relationship. In contrast, by accurately measuring the heat evolved when two protein interfaces interact, ITC directly provides not only the binding constant (K_a) and stoichiometry (n), but also the enthalpy of binding (ΔH). Additionally, ITC allows the change in Gibbs energy of the system, ΔG, and the change in entropy, ΔS, to be obtained from:

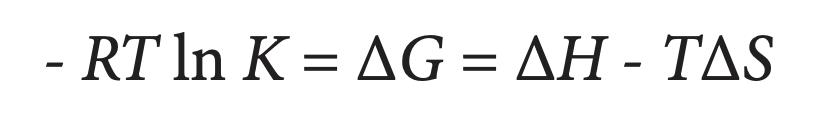
where R is the universal gas constant and T is the absolute temperature. Since enthalpic (e.g., hydrogen bonds and van der Waals interactions) and entropic (e.g., solvent mobility) contributions to the stability of a complex reflect different types of interactions, each protein complex will respond differently to environmental and mutational changes, allowing the relative importance of these interactions to be assessed (Jelesarov and Bosshard, 1999). By conducting the titration in several buffers having the same pH but different enthalpies of ionization, the enthalpy of ionization and pK of each ionizable group involved in the binding reaction can be estimated (see below). Further, by performing the experiment at two temperatures (Tl and T2), the change in heat capacity of the system, ΔC_P, can be obtained from:

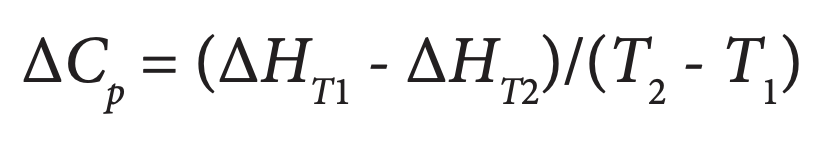
There is growing evidence that heat capacity effects reflect not only changes in hydrophobic interactions but also in hydrogen bonding and salvation as two protein surfaces interact and bind. These solvent induced heat capacity changes are considerably more substantial than previously believed, and can be significantly influenced by protonation events. Jelesarov and Bosshard (1999), Cooper (2005) and Privalov and Dragan (2006) provide detailed discussions of the physical-chemical basis underlying heat capacity changes during protein recognition and interaction. The factors that control protein binding and complex assembly are critical for designing drugs that inhibit specific proteinprotein interactions (Zhao and Chmielewski, 2005), and have heightened the importance of obtaining a complete thermodynamic description of protein folding and proteinprotein interaction processes.

Practical Considerations: Types of Protein-Protein Interactions Compatible With ITC

There are three distinct categories of protein-protein interactions: domain-domain, heteromeric, and homomeric. In domain-domain interactions, two independentlyfolded domains form an interface, often involving residues widely separated in sequence. Because domain-domain interactions occur within the same polypeptide chain,they cannot be studied by ITC experiments (which involve the titration of one component into another) unless protein fragments are used. Instead, domain-domain interactions are often probed by mutating key residues thought to be important to domain interactions, and determining the stability of the mutants by differential scanning calorimetry (DSC).

ITC is ideally suited to studying heterodimeric interactions (Velazquez-Campoy et al., 2004). A solution containing one protein (in the ITC syringe) is injected incrementally into a solution of the second protein (in the calorimetric cell). The binding or association of the two proteins with each stepwise addition of titrant releases heat proportional the concentration of the complex following injection i:

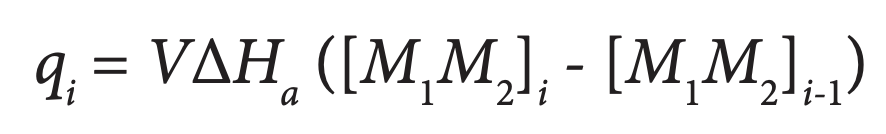
where q_i is the heat released by the ith injection, V is the volume of the cell (a constant), ΔH_a is the enthalpy of association, and [M₁ M₂]_i is the concentration of the complex after the ith injection. Titrant (M₁) is added to the second protein (M₂) until it is saturated and no further binding is observed. Since the concentrations of the two proteins are known throughout the titration, nonlinear regression analysis of qi allows calculation of ΔH_a, the binding constant (K_a=[M₁M₂]/[M₁][M₂]), and of ΔS.

ITC is also suited for studying the dissociation of homodimers. The dimeric protein is titrated into buffer in the calorimetric cell, where dilution of the protein leads to dissociation into its constituent subunits (Velazquez-Campoy et al., 2004). The dissociation constant K_d determines the distribution of the subunits between the monomeric (M) and dimeric (M₂) states (K_d = [M]²/[M₂]). Since the heat associated with each injection of protein (q_i) is proportional to the concentration of monomer after the ith injection, the enthalpy due to the dissociation of the protein into monomers (ΔH_d) can be determined by:

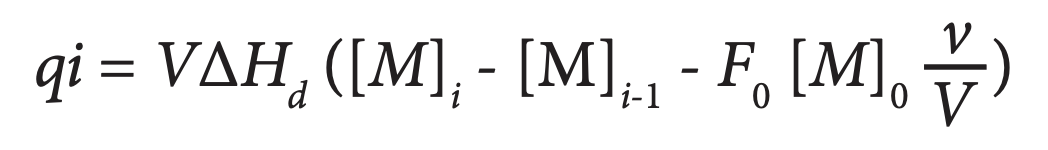
where V is again the volume of the calorimetric cell, v is the injection volume, [M]₀ is the concentration of protein in the cell (on a per monomer basis), and F₀, a correction factor, is the fraction of monomer present in the dimer solution in the syringe (since dimers always exist in equilibrium with monomers). As the titration proceeds and the monomer concentration in the cell increases, the dissociation reaction becomes increasingly less favorable until finally, further injections of dimer produce no significant heat. The dissociation constant, the enthalpy due to dissociation and the entropy can then be determined by nonlinear regression analysis.

Concentration Ranges Compatible With ITC

Since equilibrium processes involve the reversible interconversion of two components (such as two proteins to a protein complex, or a dimer to monomers), experiments must be conducted at appropriate concentrations so that a change in the concentration of one component leads to a measurable change in the concentration of the second component. For binding experiments in which two proteins interact, concentrations should be chosen so that during approximately the first third of the titration, essentially all the titrant binds to the macromolecule in the cell, and during the last third of the titration, the macromolecule is essentially saturated with titrant and little or no further binding occurs. When heat vs. [M₁]/[M₂] is plotted, the curvature in the center of the plot (between these two extremes) allows accurate determination of the enthalpy and the association constant for the binding reaction. These conditions are generally achieved if concentrations are chosen so that:

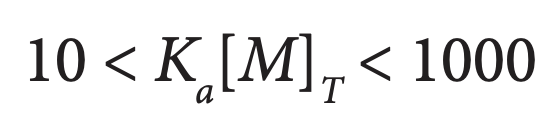
where [M]_T is the total concentration of the macromolecule in the reaction cell. Binding constants in the order of 10² – 10⁹ M^-1 can be accurately calculated; binding constants for systems with tighter binding can often be estimated by performing the titration at suboptimal pH or temperature, and then extrapolating K_a to the desired conditions (Doyle et al., 1995; Doyle and Hensley, 1998; Velazuqez-Campoy and Freire, 2005). Alternatively, accurate determinations of very high or low binding constants can be obtained through competitive binding experiments.

If an accurate determination of the enthalpy of binding is of primary importance, the ‘titrant’ protein should be injected into a large excess of the ‘binding’ protein in the sample cell. Although neither the binding constant or the stoichiometry of binding can be determined from this experiment (since no saturation of the binding site will occur), the binding heat can be very accurately measured following subtraction of a blank run designed to compensate for dilution effects, buffer mismatch, etc. (Jelesarov & Bosshard, 1999; O’Brien et al., 2001).

The dissociation of dimeric proteins with dissociation constants in the range 10^-3 – 10^-7 M can be determined by ITC if the experiments are conducted at concentrations so that [M₂]_T/K_d lies between 10 and 10,000 (Velazquez-Campoy and Freire, 2004), where [M₂]_T is the total concentration of dimer in the syringe. This restriction is due to the fact that if the dissociation constant is very low, protein injected into buffer in the sample cell will result in the formation of only a small number of monomers and thus little heat will be observed; alternatively, if the dissociation constant is very high, few dimers will be present in the syringe, so again little heat will be observed upon dilution. If no prior information on the dissociation constant is available from which to estimate K_d, a trial and error approach will be required to establish concentrations compatible with obtaining useful ITC data.

Practical Example: Characterization of Heterodimer Formation

The application of ITC for characterizing heterodimer formation is illustrated by the example of soybean trypsin inhibitor binding to porcine pancreatic trypsin. In order to obtain a titration curve with sufficient points for accurate curve fitting, titrant should be incrementally added until it exceeds stoichiometric binding to the second protein. This trypsin/inhibitor binding experiment was designed using Experiment Design Wizard, the data simulation module included in the analysis software, NanoAnalyze™. This module allows experimental parameters such as concentration and anticipated thermodynamic results to be input, and outputs a simulation of the expected experimental thermogram. Using this module prior to any laboratory experimentation ensures that time and sample material are not wasted on runs that cannot produce useable data due to improper concentration choices.

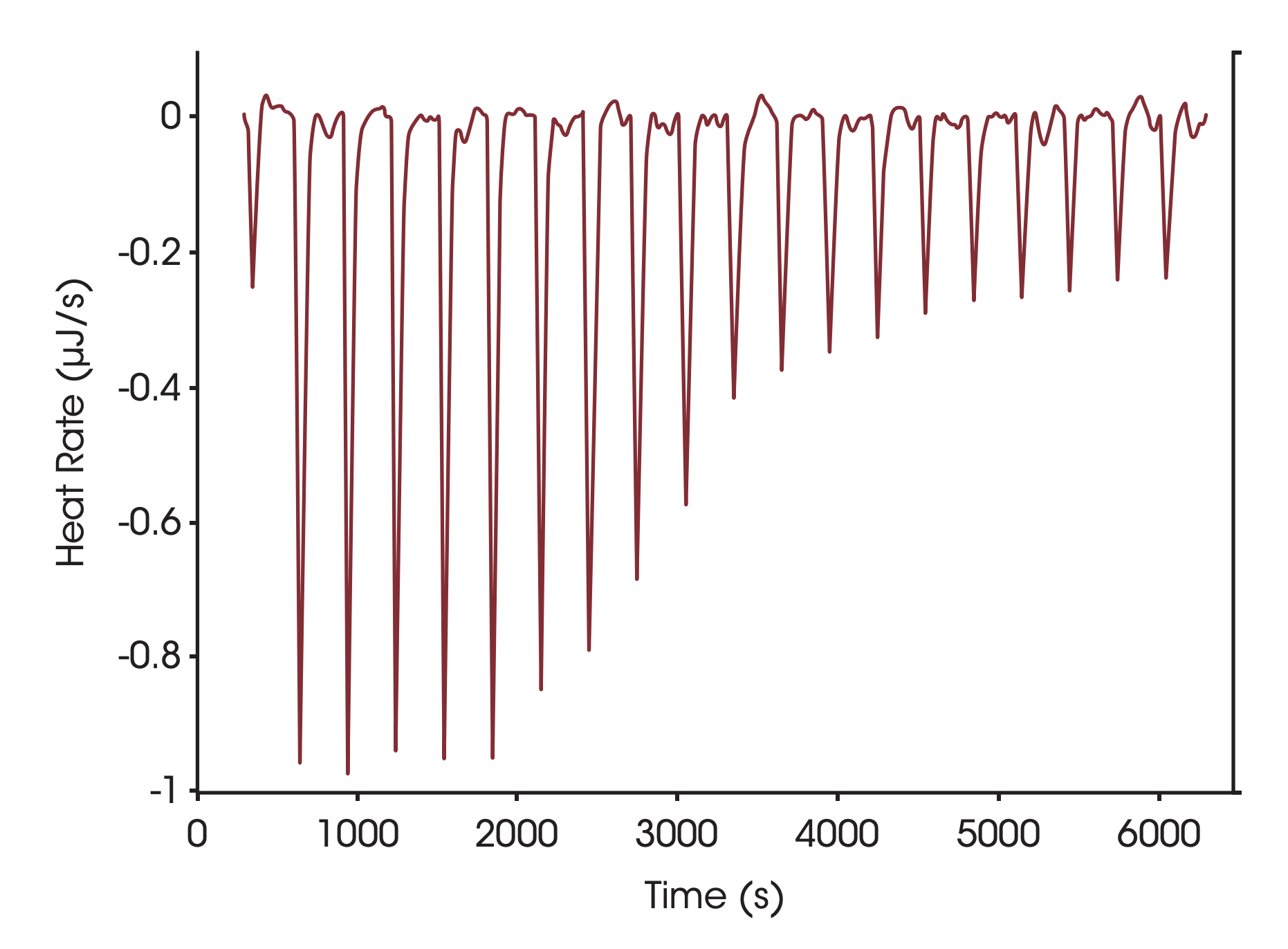
Conditions used to determine the stoichiometry of binding, the binding enthalpy and the association constant for soybean trypsin inhibitor binding to trypsin are shown in Fig. 1. The sigmiodal shape of the curve in Fig 1 and the numerous points throughout the curved portion of the plot facilitates estimation of the midpoint of the transition, and thus the stoichiometry of the binding reaction. K_a and ΔH are calculated by iterative approximation; all calculations are performed automatically by the data analysis module, NanoAnalyze™. Optimal binding of soybean trypsin inhibitor to trypsin occurs at pH 8, with a binding constant on the order of 10¹¹ M^-1 (Velazquez-Campoy et al., 2004). The present titration was conducted at 25 °C, pH 4.5 in order to decrease the affinity to a level compatible with ITC (range 10² – 109 M-1). Under these conditions, the proteins bind endothermically with an enthalpy of 135 KJ mol^-1 and a K_a of 1.4 x 10⁷. It is possible to estimate the heat capacity change upon association by repeating the titration at several temperatures and plotting the enthalpy of association vs. temperature; the slope of the plot corresponds to the change in heat capacity due to association. A positive value is indicative of protein surface being exposed to solvent when two proteins interact (which is more likely to occur when two proteins dissociate rather then bind), whereas a negative value reflects the dehydration of protein surfaces (Privalov and Dragan, 2006).

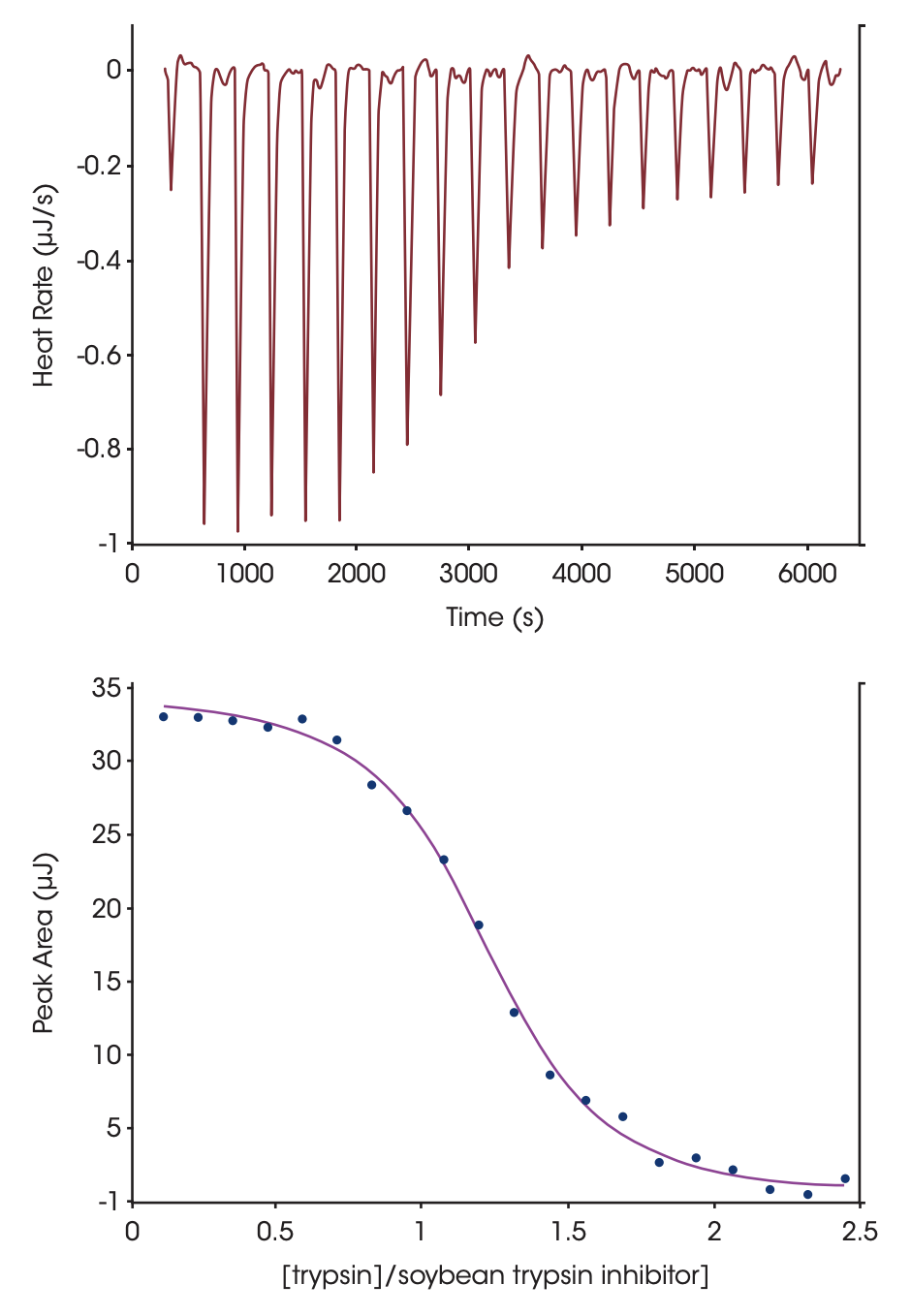
Figure 1. Titration of porcine pancreatic trypsin into soybean tripsin inhibitor using a CSC model 5300 ITC-III. Both proteins were dialyzed at 4 °C against 25mM potassium acetate pH 4.5 buffer containing 10 mM calcium chloride. Soybean tripsin inhibitor (2.1 μM) was loaded in the 1.0 mL sample cell and trypsin (440 μM) was loaded in the 100 μL syringe. Twenty, 5 μL aliquots of ligand were titrated into the sample cell while the temperature of the system was maintained at 25 °C. Top panel: The signal (heat) produced following each addition of protein to the inhibitor. Bottom panel: Integration of the heats over the time course of the experiment; the μJ in each peak are plotted against the mole ratio of the titrant (trypsin) to inhibitor (soybean trypsin inhibitor). The inhibitor was placed in the sample cell rather than the syringe due to its low solubility. K_a of binding: 1.4 x 10⁷; stoichiometry: 1.15; enthalpy of binding: 135 KJ mol^-1. Note that the major source of error in determining stoichiometry is accurate knowledge of the reactant concentrations.

Protonation Effects

When two protein interfaces bind, the pKa values of ionizable groups at the interfaces can be altered due to solvation or electrostatic changes triggered by the binding event, resulting in protonation or deprotonation of these residues. If this occurs, the association constant will be pH-dependent, and the binding enthalpy will be dependent on the ionization enthalpy of the buffer (ΔH_buf). A series of ITC experiments can establish whether a protonation / deprotonation reaction is occurring and if so, how many protons are involved. If independent structural information about the interacting residues in the complex is available, individual contributions of specific amino acids to the binding reaction can be determined, allowing a thermodynamic mapping of the binding interface (Gomez and Freire, 1995; Frisch et al., 1997; Crnogorac et al., 2001)

The ITC titrations are performed in buffers with different ionization enthalpies. The measured enthalpy, ΔH_app, is equal to the enthalpy of binding (ΔH_bind, which is independent of the buffer used, but is p_H dependent), to nH,the number of protons adsorbed or released by the binding reaction, and to the ionization enthalpy of the buffer:

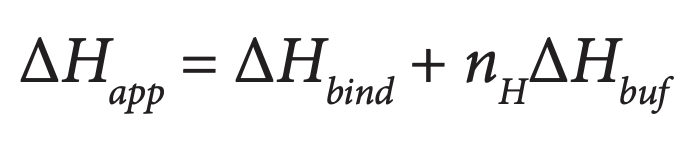
The buffer ionization enthalpy can be obtained from tables (Christensen et al., 1976), measured (Jelesarov and Bosshard, 1994) or obtained from the papers cited below. A plot of ΔH_app vs. the buffer ionization enthalpy will provide a straight line from which n_H can be estimated from the slope and ΔH_bind from the intercept with the y axis. If the slope is zero then there is no net transfer of protons, if n_H is positive then protons are transferred from the buffer solvent to the protein complex, and if n_H is negative, then protons are transferred from the complex to the solvent. The enthalpy of ionization and the pK_a of each ionizable group involved in the protonation / deprotonation reaction can be calculated using the approach developed by Baker and Murphy (1996 and 1997) and Gomez and Freire (1995). This approach has been used to quantify the binding energetics of closely-related inhibitors (Parker et al., 1999), the displacement of ligands (Ciaccio et al., 2004) and competing metals (Christensen et al., 2003), and the identification of charged groups involved in binding drugs to proteins and DNA (Velazquez-Campoy et al., 2000; Kaul et al., 2003; Lobo et al., 2003; Barbieri and Pilch, 2006; Nguyen et al., 2006).