Keywords: TMA, Thermomechanical Analysis, VICAT, Temperature under load, PVC
TA138
Summary
Deflection Temperature Under Load (DTUL) and VICAT softening are two methods widely used by the American Society for Testing and Materials (ASTM) to project material performance. However, these methods require large samples and are time consuming. Thermomechanical analysis (TMA), which measures dimensional change with temperature, provides a rapid, easy-to-use alternative to these ASTM methods.
Introduction
ASTM and other quality control oriented organizations have developed many tests for determining the modulus of polymers. DTUL and VICAT softening are two of the ASTM methods which have been accepted standards for many years. Both of these tests, however, suffer from serious shortcomings. First, they require large quantities of material, usually in the form of compression molded sheets, which makes it difficult to analyze small lab preparations of new materials. Second, the tests are run at two degrees per minute or slower, which makes the analysis time very long. Third, in actual use, the tests are performed on starting material and not on the end product, not taking into consideration any changes during processing.
Recently there has been increased interest in the use of Thermomechanical Analysis (TMA) to replace these tests since smaller quantities of sample are required, higher heating rates are possible, and samples can be analyzed before and after processing. Yanai, Freund and Carter at the Rohm and Haas Company (1), have demonstrated a definite correlation between the data from the accepted ASTM methods and that obtained by TMA.
Experimental
In TMA, the material’s dimensional change is measured while the material is subjected to controlled heating or cooling. Several sample configurations are available for measuring this dimensional change on a wide variety of material types and forms. In the penetration configuration, for example, the probe has a small diameter tip for concentrating the applied force on a specific section of the material’s surface. The penetration probe is commonly used to determine transition temperatures such as the glass transition and the softening points. However, since the probe geometry is well-defined and the applied force (loading) can be precisely controlled, it is possible to obtain additional information from penetration experiments including modulus, DTUL, and VICAT softening as shown in the study by Carter and his coworkers. The TMA results in that study were obtained using 0.20 in. x 0.20 in. x 0.10 in. samples heated at 5°C/minute.
Results
Deflection Temperature Under Load (DTUL)
The Young’s Modulus of a material may be determined as a function of temperature by following the penetration of a weighted probe into a sample as the sample is heated at a uniform rate. The equation to be used to make this determination is:
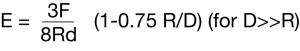
where:
E = Young’s Modulus (kg/cm2)
F = the load on the probe (kg)
R = the radius of the probe (cm)
d = the depth of penetration of the probe at some temperature (cm) D = the thickness of the sample (cm)
The DTUL is determined in the ASTM method (2) by applying a load to the center of a sample which acts as a beam supported at both ends. The Young’s Modulus of this beam can be calculated using the equation:
where:
C = the width of the sample (cm)
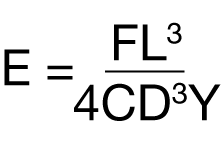
L = the length of the sample between the beam supports (cm) D = the thickness of the sample (cm)
F = the load on the sample (kg)
Y = the deflection of the sample under load (cm)
The DTUL is defined to be the temperature at which a sample of specified dimensions (C,L,D) under a specified load (F) has a given deflection (Y). The DTUL is, therefore, the temperature at which a material has a certain predefined Young’s Modulus.
The DTUL is normally determined at one of two loading levels, 18.5 and 4.6 kg/cm2 (264 and 66 psi) The 18.5 kg/cm2 loading level, corresponding to a Young’s Modulus of 9.7 x 103 kg/cm2, was selected.
The above value of Young’s Modulus was substituted into the equation for E to be used with a weighted probe. With this information it was possible to calculate the required penetration of the probe at the DTUL temperature.
The penetration necessary, using a 0.025 in. diameter penetration probe and a load of 10 gm, was calculated to be extremely small (5 x 10-6 in.) at the DTUL Young’s Modulus. It was decided, therefore, to take the DTUL temperature as the point where the displacement vs. temperature plot of the TMA left the baseline. For the purpose of their study, the baseline was defined by the straight line expansion of the material before any detectable penetration.
Four samples of modified and unmodified PVC, on which DTUL data has been obtained, were examined using the probe penetration method. As shown in Table 1, there is very good agreement between the ASTM DTUL temperature and the first deviation from the baseline of the TMA penetration vs. temperature plot.
Table 1. Deflection Temperature Under Load
| Sample | TMA ºC | ASTM ºC |
|---|---|---|
| Unmodified PVC | 73 | 75 |
| Service Temp. Mod. PVC | 90 | 91 |
| Impact Mod. PVC | 73 | 73 |
| Service Temp. & Impact Mod. PVC | 78 | 80 |
VICAT Softening Temperature
The VICAT softening temperature is defined by ASTM (3) as the temperature at which a circular probe of 1.0 mm2 cross-section, under load of 1000 gm, penetrates 1.0 mm into a sample 12.7 mm thick.
By substituting this information into the penetration equation, the Young’s Modulus at the VICAT Softening Temperature was found to be 66 kg/cm2.
Plots of penetration vs. temperature for the modified and unmodified PVC used to determine DTUL were reexamined, and the temperatures corresponding to a modulus of 66 kg/ cm2 were obtained. This corresponded to a penetration of 6.4 x 10-4 in. with a 0.025 in. diameter probe and a load of 10 gm.
Table 2 shows the excellent agreement of the TMA temperatures with the VICAT temperatures obtained by the standard ASTM method.
Table 2. VICAT Softening Temperature
| Sample | TMA ºC | ASTM ºC |
|---|---|---|
| Unmodified PVC | 86 | 84 |
| Service Temp. Mod. PVC | 106 | 103 |
| Impact Mod. PVC | 84 | 85 |
| Service Temp. & Impact Mod. PVC | 93 | 92 |
References
- Carter, O.L. et. al., Thermomechanica Acta 4, p.199-202 (1972)
- ASTM Standards, ASTM, Philadelphia, Pa, section 8, April 1987 D-648, p.249
- ASTM Standards, ASTM, Philadelphia, Pa, section 8, April 1987 D-1525, p.527
Acknowledgement
Click here to download the printable version of this application note.

