Stichwörter: Batterie, Elektrode, thermische Analyse, Wärmeleitfähigkeit
TPP036-DE
Abstract
Eine effektive Überwachung der Temperatur einer Lithium-Ionen-Batteriezelle setzt die Kenntnis der thermischen Eigenschaften der Batteriekomponenten voraus. Eigenschaften wie Wärmekapazität, Wärmeleitfähigkeit und Temperaturleitfähigkeit charakterisieren die Wärmeübertragung zwischen einzelnen Materialien und Verbundmaterial in der Zelle. Diese Parameter sind entscheidend für die Entwicklung des thermischen Batteriemodells und den Aufbau des Thermomanagementsystems. Die Wärmeleitfähigkeit dünner Komponenten, wie sie beispielsweise in der Elektrode verwendet werden, lässt sich durch Messungen der Temperaturleitfähigkeit und der Wärmekapazität bestimmen. In diesem Artikel wird die Methodik zur Messung der Wärmeleitfähigkeit eines auf einen dünnen Kupferstromkollektor aufgetragenen Batterie-Anodenmaterials betrachtet, deren Ergebnisse für die Entwicklung, Optimierung und Gestaltung von Batterie-Thermomanagementsystemen relevant sind.
Einführung
Batterie-Thermomanagementsysteme (Battery Thermal Management System, BTMS) werden zur Aufrechterhaltung der Temperatur von Lithium-Ionen-Batterien (LIB) eingesetzt und sind daher von entscheidender Bedeutung für deren Sicherheit und Funktion. Ein effektives Batterie-Thermomanagementsystem kann die Lebensdauer der Batterie verlängern, die Leistung bei Kälte verbessern und gravierende Sicherheitsrisiken durch Überhitzung und thermisches Durchgehen verhindern [1]. Beim Design des Batterie-Thermomanagementsystems ist zu berücksichtigen, wie jede Komponente der Zelle während des Batteriebetriebs Wärme ableitet. Beispielsweise kommt es in der Elektrode und im Stromkollektor beim Laden und Entladen der Batterie zu einer Erwärmung, da Ionen zwischen der Elektrode und dem Stromkollektor ausgetauscht werden. Die Geschwindigkeit der Wärmeübertragung hat direkte Auswirkungen auf die Temperaturschwankungen der Batteriezelle. Die Kenntnis der thermischen Eigenschaften der Elektrode, wie z. B. Temperaturleitfähigkeit, Wärmeleitfähigkeit und spezifische Wärmekapazität, ist eine Voraussetzung dafür, dass diese Wärme effektiv abgeleitet werden kann [2].
Die Temperaturleitfähigkeit, d. h. die Geschwindigkeit, mit der sich Wärme durch ein Material hindurch ausbreitet, kann Aufschluss über die Gewichtung der thermischen und elektrischen Leistung von Elektrodenmaterial geben [3] [4]. Die Wärmeleitfähigkeit und Wärmekapazität der Anode und des Stromkollektors sind ebenfalls wichtige Eigenschaften bei der Gestaltung und beim Aufbau des Batterie-Thermomanagementsystems [5]. Die mit der Laser-Flash-Methode gemessene Diffusivität kann in Kombination mit Wärmekapazitätsmessungen mittels dynamischer Differenzkalorimetrie (Differential Scanning Calorimetry, DSC) zur Bestimmung der Wärmeleitfähigkeit von Anodenmaterialien verwendet werden.
Praktischer Nutzen
- Analyse der thermischen Eigenschaften von Batteriematerial zur Entwicklung thermischer Modelle
- Messung komplexer, dünner Anodenmaterialien mit Lichtpuls-Techniken, zum Beispiel mit dem Discovery™ Xenon Flash 200+ von TA Instruments™, zur Quantifizierung schneller Wärmeübertragung
- Einfache Bestimmung der materialspezifischen Wärmekapazität mit einem dynamischen Differenzkalorimeter der Reihe Discovery von TA Instruments
- Bestimmung der Wärmeleitfähigkeit dünner Anoden-Proben aus mehreren Komponenten mithilfe von Messungen der Temperaturleitfähigkeit und der Wärmekapazität
Experimente
Es wurden Messungen der Temperaturleitfähigkeit (α), der spezifischen Wärmekapazität (Cp) und der Wärmeleitfähigkeit (λ) einer Folie aus Anodenmaterial und einer unbeschichteten Kupferprobe bei 25 °C durchgeführt. Das Anodenmaterial bestand hauptsächlich aus Graphit mit Carbon Black, Carboxymethylcellulose (CMC) und Styrol-Butadien-Kautschuk (Styrene-Butadiene Rubber, SBR) und wurde auf einen Stromkollektor aus dünner Kupferfolie aufgetragen. Eine unbeschichtete Kupferfolie des gleichen Typs und der gleichen Stärke wurde als Kontrolle ebenfalls analysiert („unbeschichtetes Kupfer“). Das unbeschichtete Kupfer hatte eine Stärke von 0,009 mm, und die Anodenprobe hatte eine Stärke von 0,12 mm.
Bei Proben mit hoher Wärmeleitfähigkeit wird die Temperaturleitfähigkeit mit der Laser-Flash-Methode gemessen. Bei beiden Proben wurde dazu ein Discovery Xenon Flash 200+ (DXF 200+) Lichtpuls-Analysator von TA Instruments™ verwendet. Bei der Flash-Methode wird die Oberfläche einer Probe normalerweise einem kurzen Energieimpuls ausgesetzt. Zur Bestimmung der Temperaturleitfähigkeit der Probe wird dann die Dissipation der Energie durch die Probe über eine von der Software vorgegebene Strecke aufgezeichnet. Beim Testen dünner Proben in einem Lichtpuls-Analysator kann die Diffusivität nicht in der Standardrichtung senkrecht zur Fläche gemessen werden („Through-Plane“). Stattdessen werden dünne Proben horizontal über die Probenfläche gemessen („In-Plane“). Dazu wird eine spezielle In-Plane-Halterung verwendet (Abbildung 1), in der die Folie zwischen zwei Masken eingespannt wird, sodass die Pulsenergie konzentrisch nach innen in Richtung Probenmitte fließen kann. Der äußere Rand wird von unterhalb der Probe durch einen Puls erhitzt und die Detektion erfolgt an der Oberseite der Probe. Beide Proben wurden zu Rundstücken mit einem Durchmesser von 25,4 mm gestanzt und so in der In-Plane-Halterung befestigt.

Stark reflektierende Oberflächen streuen das Licht, sodass die Probe kaum ausreichend Energie aus dem Puls aufnehmen kann, um ein ausreichendes Signal zu erzeugen. Daher werden reflektierende Proben für Flash-Messungen mit einer dünnen Schicht Graphit besprüht. Für diese Arbeit wurde die Unterseite jeder Probe mit einer dünnen Schicht Graphit besprüht und die Oberseite wurde mit einer dünnen Schicht Silberfarbe überzogen, um einen guten Stiftkontakt zu gewährleisten, Rauschen zu minimieren und genaue Ergebnisse zu erzielen. Das Anodenmaterial und die unbeschichteten Kupferproben wurden im In-Plane-Modus gemessen, und aus drei separaten Pulsen wurde die durchschnittliche Temperaturleitfähigkeit ermittelt.
Bei In-Plane-Tests sind separate Wärmekapazitätsmessungen erforderlich, um Wärmeleitfähigkeitswerte zu erhalten. Bei bekannter Dichte, Temperaturleitfähigkeit und spezifischer Wärmekapazität einer Probe kann die Wärmeleitfähigkeit des Materials berechnet werden. Zur Bestimmung der spezifischen Wärmekapazität der unbeschichteten Kupferproben und der Anodenmaterialproben wurde modulierte dynamische Differenzkalorimetrie (Modulated Differential Scanning Calorimetry, MDSC) [6] verwendet. Die Experimente wurden auf einem Discovery DSC 2500 mit einem Probengewicht von 22 mg (± 2 mg) in Tzero® Aluminiumtiegeln mit Standarddeckel durchgeführt. Die Temperatur bei der modulierten dynamischen Differenzkalorimetrie wurde bei beiden Proben von unter Raumtemperatur auf etwas darüber erhöht, um einen stetigen Wärmefluss bei der für diese Berechnung relevanten Temperatur von 25 °C zu gewährleisten. Die Proben wurden über einen Zeitraum von 120 Sekunden mit einer sinusförmigen Modulation von ± 1 °C von 5 °C auf 40 °C erhitzt (durchschnittliche Erwärmungsgeschwindigkeit: 1 °C/min). Zur Kalibrierung und Validierung der Wärmekapazitätswerte des Geräts mit dieser modulierten Methode wurde ein Saphirstandard verwendet.
Ergebnisse und Diskussion
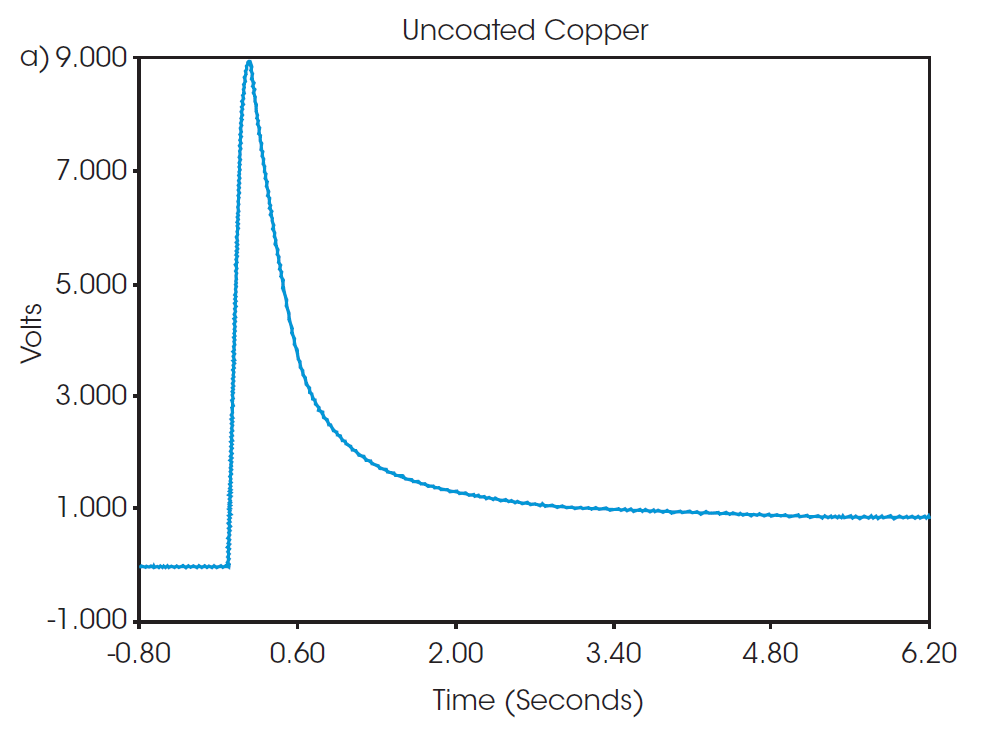
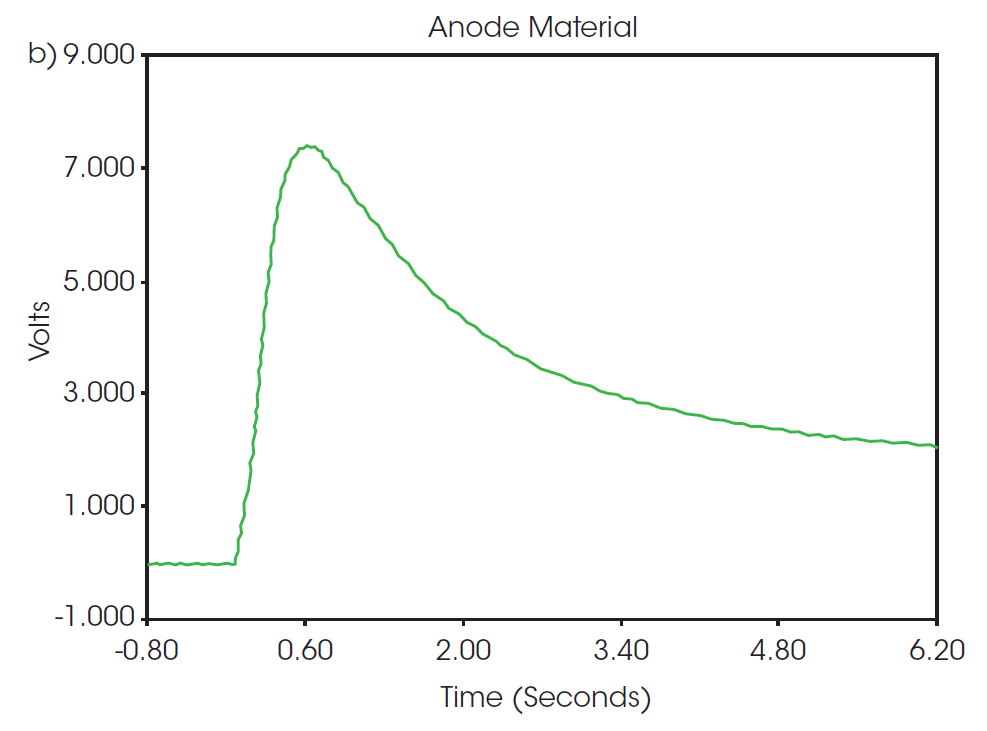
In Abbildung 2 sind repräsentative Thermogramme der Flash-Pulse beider Proben dargestellt. Die beobachteten Formen der Thermogramme sind typisch für die Reaktion auf einen Flash-Puls und weisen sehr wenig Rauschen auf, sodass die Zuverlässigkeit der Ergebnisse als hoch zu betrachten ist. Intensität, Dauer und Dissipation der Reaktion auf den Puls werden zur Berechnung der Temperaturleitfähigkeit verwendet, indem die Daten wie zuvor beschrieben an ein Modell angepasst werden, das auf einer Näherungsgleichung für den Wirkungsgrad von Rippen basiert [7]. Wie sich aus den Ergebnissen der drei Pulsmessungen ergab, betrug die Temperaturleitfähigkeit des unbeschichteten Kupfers bei 25 °C 1,194 cm2/s und des Anodenmaterials 0,371 cm2/s (Tabelle 1).
Tabelle 1. Temperaturleitfähigkeit bei jedem Puls im DXF 200+ Experiment
| Puls | Temperaturleitfähigkeit (cm2/s) | |
|---|---|---|
| Unbeschichtetes Kupfer | Anodenmaterial | |
| 1 | 1.193 | 0.363 |
| 2 | 1.195 | 0.379 |
| 3 | 1.194 | 0.371 |
Die in dem Experiment mit modulierter dynamischer Differenzkalorimetrie gemessene spezifische Wärmekapazität als Funktion der Temperatur ist in Abbildung 3 dargestellt. Die spezifische Wärmekapazität der unbeschichteten Kupfer- und der Anodenproben beträgt 0,3827 bzw. 0,5868 J/g°C bei 25 °C. Im Vergleich zu der unbeschichteten Kupferprobe weist das Anodenmaterial eine höhere Gesamtwärmekapazität und eine größere temperaturbedingte Veränderung auf. Der aufgezeichnete Wert für die spezifische Wärmekapazität des Anodenmaterials bezieht sich auf die gesamte Anordnung von Graphit und anderen Zusatzstoffen, die auf der Oberfläche einer Kupferfolie abgelagert sind, und nicht auf die Eigenschaft eines einzelnen Materials. Faktoren wie die Qualität des Beschichtungsauftrags und die Mischung der Zusammensetzung können die thermische Leistung der Komponente insgesamt beeinflussen. Die direkte Messung der Eigenschaften des gesamten Systems liefert ein besseres Bild der thermischen Leistung insgesamt als es bei einer Einschätzung auf der Grundlage der Zusammensetzung der Fall wäre.
Die Wärmeleitfähigkeit jeder Probe kann mit Gleichung 1 berechnet werden.
λ = α *Cp * ρ (1)
mit:
- λ = Wärmeleitfähigkeit (W/m·K)
- α = Temperaturleitfähigkeit (m2/s)
- Cp = spezifische Wärmekapazität (J/kg·K)
- ρ = Dichte (kg/m3)
Unbeschichtetes Kupfer hat eine Dichte von 8,940 g/cm3, und das Anodenmaterial hat eine berechnete Dichte von 1,959 g/cm3. Die unbeschichtete Kupferprobe wies eine Wärmeleitfähigkeit von 408,6 W/m·K auf, das Graphit-Anodenmaterial hatte insgesamt eine Wärmeleitfähigkeit von 42,64 W/m·K.
Obwohl Graphit der Hauptbestandteil ist, ist es wichtig zu bedenken, dass das Anodenmaterial auch noch verschiedene Polymerzusätze und Füllstoffe enthält, die auf einer dünnen Kupferfolie abgeschieden sind. Sowohl diese Materialmischung als auch der Zwischenschichtraum zwischen Anodenfolie und Kupferfolie tragen zu der gemessenen Temperaturleitfähigkeit und berechneten Wärmeleitfähigkeit für das Anodenmaterial bei (zusammengefasst in Tabelle 2). Unterschiedliche Formulierungen der Anode wirken sich auf die resultierende Leitfähigkeit aus, und diese Messungen können zur Optimierung der jeweiligen Zusammensetzung verwendet werden. Darüber hinaus sollte bei der Verwendung komplexer Formulierungen die Wärmeleitfähigkeit experimentell bestimmt werden, um den bestmöglichen Input für die Einschätzung der thermischen Leistung der Batterie insgesamt und die Entwicklung des Batterie-Thermomanagementsystems zu erhalten.
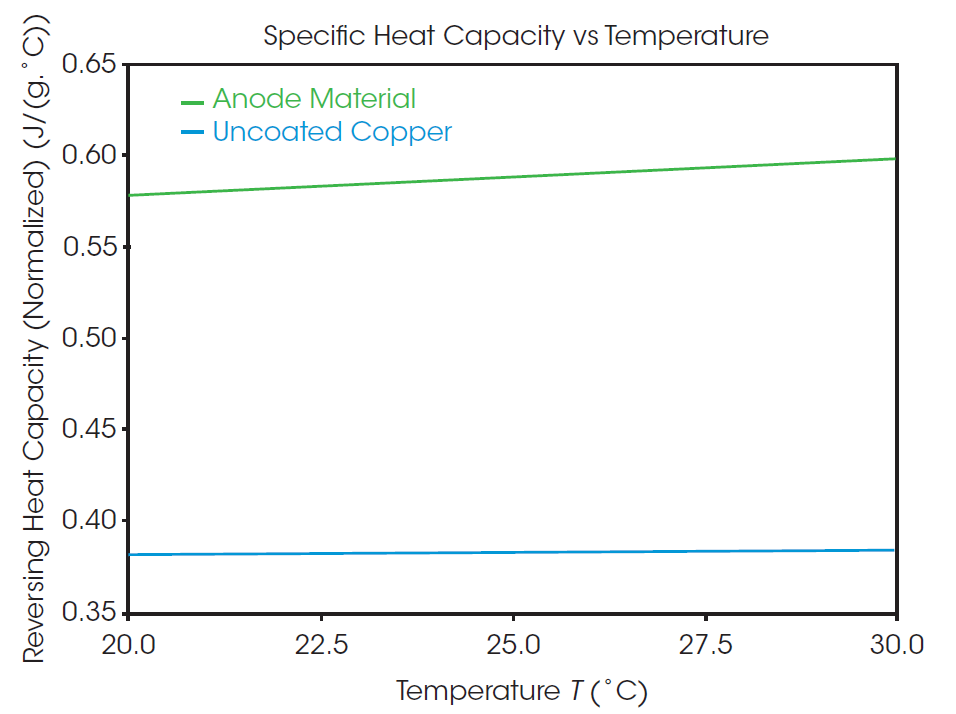
Tabelle 2. Zusammenfassung der thermischen Eigenschaften der Anode und unbeschichteter Proben
| Unbeschichtetes Kupfer | Anodenmaterial | |
|---|---|---|
| Temperaturleitfähigkeit (cm2/s) | 1.194×10-4 | 0.371 x10-4 |
| Spezifische Wärmekapazität (J/kg·K) | 382.7 | 586.8 |
| Dichte (kg/m3) | 8940 | 1959 |
| Wärmeleitfähigkeit (W/m·K) | 408.6 | 42.64 |
Fazit
Das Batterie-Thermomanagementsystem erfordert genaue Messungen der thermischen Eigenschaften. Mit einem DXF 200+ und einem Discovery 2500 DSC wurde die Wärmeleitfähigkeit einer LIB-Anode auf Graphitbasis, beschichtet auf einen Kupferstromkollektor, gemessen und mit der eines unbeschichteten Kupferstromkollektors verglichen. Zur Berechnung der Wärmeleitfähigkeit wurden die Materialdichte, die mit dem DXF gemessene Temperaturleitfähigkeit und die mit dem DSC gemessene spezifische Wärmekapazität herangezogen. Zur Bestimmung der Temperaturleitfähigkeit der Proben wurden Flash-Messungen in In-Plane-Richtung durchgeführt. Die spezifische Wärmekapazität wurde mittels modulierter dynamischer Differenzkalorimetrie als Funktion der Temperatur gemessen. Die zusätzliche Anodenbeschichtung auf den Kupferstromkollektor ergab eine Wärmeleitfähigkeit, die fast eine Größenordnung niedriger war als die des unbeschichteten Kupfers. Das Anodenmaterial bestand zwar überwiegend aus Graphit, enthielt aber auch Carbon Black und Polymerzusätze, die sich auf die thermischen Eigenschaften auswirken können. Die Mischung und das Aufbringen der Beschichtung auf den Kollektor kann die thermische Leistung weiter beeinflussen, sodass für die Optimierung der Anodenzusammensetzung, die Modellerstellung und die Klärung der Auswirkungen auf Thermomanagementsysteme in Batterien Messungen der gesamten Komponente durchgeführt werden sollten.
Literaturhinweise
- Q. Zheng, M. Hao, R. Miao, J. Schaadt and C. Dames, “Advances in thermal conductivity for energy applications: a review,” Progress in Energy, 2021.
- M. Steinhardt, J. V. Barreras, H. Ruan, B. Wu, G. J. Offer and A. Jossen, “Meta-analysis of experimental results for heat capacity and thermal conductivity in lithium-ion batteries: A critical review,” Journal of Power Sources, vol. 522, 2022.
- Q. Ma, “TPP034: In-Plane Measurement of Thermal Diffusivity of Copper Thin FIlm,” TA Instruments, New Castle, DE, 2022.
- Q. Ma, “TPP035: In-Plane Measurement of Thermal Diffusivity of Graphite Thin Film,” TA Instruments, New Castle, DE, 2022.
- D. Werner, A. Loges, D. J. Becker and T. Wetzel, “Thermal conductivity of Li-ion batteries and their electrode configurations- A novel combination of modelling and experimental approach,” Journal of Power Sources, vol. 364, pp. 72-83, 2017.
- Y. Schuman, “Heat Capacity Measurements Using Modulated DSC (MDSC) – Both Ramping and Quasi-isothermal Methods,” TA Instruments, New Castle, DE.
- J. Gembarovic, H. Wang and D. Paganelli, “A New Fin Model on In-Plane Thermal Diffusivity Measurement of Thin Films by the Flash Method,” in International Heat Transfer Conference 16, Beijing, China, 2018.
Danksagung
Diese Veröffentlichung wurde von Andrew Janisse, PhD, Justin Wynn, Applications Specialist, Jennifer Vail, PhD, bei TA Instruments verfasst.
Hier klicken, um eine Druckversion dieses Anwendungsartikels herunterzuladen.

